Last Updated on October 22, 2023 by pm_author_91ksj
When it comes to identifying a local minimum of a graphed function, it’s important to understand the concept and its significance. A local minimum refers to the lowest point within a specific interval of a function. It represents a point where the function is at its lowest value compared to the surrounding points. By correctly identifying this point, we can gain insights into the behavior and characteristics of the function.
To determine a local minimum, we need to analyze the behavior of the function in the vicinity of a particular point. This involves examining the slope of the function and its concavity. A local minimum occurs when the slope changes from negative to positive and the concavity changes from concave down to concave up. By observing these key indicators, we can accurately identify the local minimum of a graphed function.
Which Statement Correctly Identifies a Local Minimum of The Graphed Function?
What is a Local Minimum?
A local minimum is a crucial concept in analyzing the behavior of a function. It refers to the lowest point within a specific interval of a function. Understanding this concept allows us to gain insights into the characteristics and behavior of the function.
Identifying a Local Minimum on a Graph
To identify a local minimum on a graphed function, we must analyze the slope and concavity of the function. A local minimum occurs when the slope changes from negative to positive and the concavity changes from concave down to concave up.
Here are the steps to identify a local minimum on a graph:
- Determine the intervals where the function is decreasing. This can be done by analyzing the slopes of the function. If the slope is negative, it means the function is decreasing.
- Look for points where the function changes from decreasing to increasing. These points indicate a possible local minimum.
- Check the concavity of the function at these points. If the concavity changes from concave down to concave up, it confirms the presence of a local minimum.
- Verify that the identified point is indeed the lowest point within the specific interval by comparing it to the values of neighboring points.
By following these steps, we can correctly identify a local minimum on a graphed function. This knowledge is essential in various mathematical applications, including optimization problems, as it allows us to make informed decisions and predictions about the behavior of the function.
Understanding the concept of a local minimum empowers us to delve deeper into the behavior of functions and enables us to solve mathematical problems more effectively. It is a fundamental concept in mathematics and optimization, providing valuable insights into the characteristics of functions.
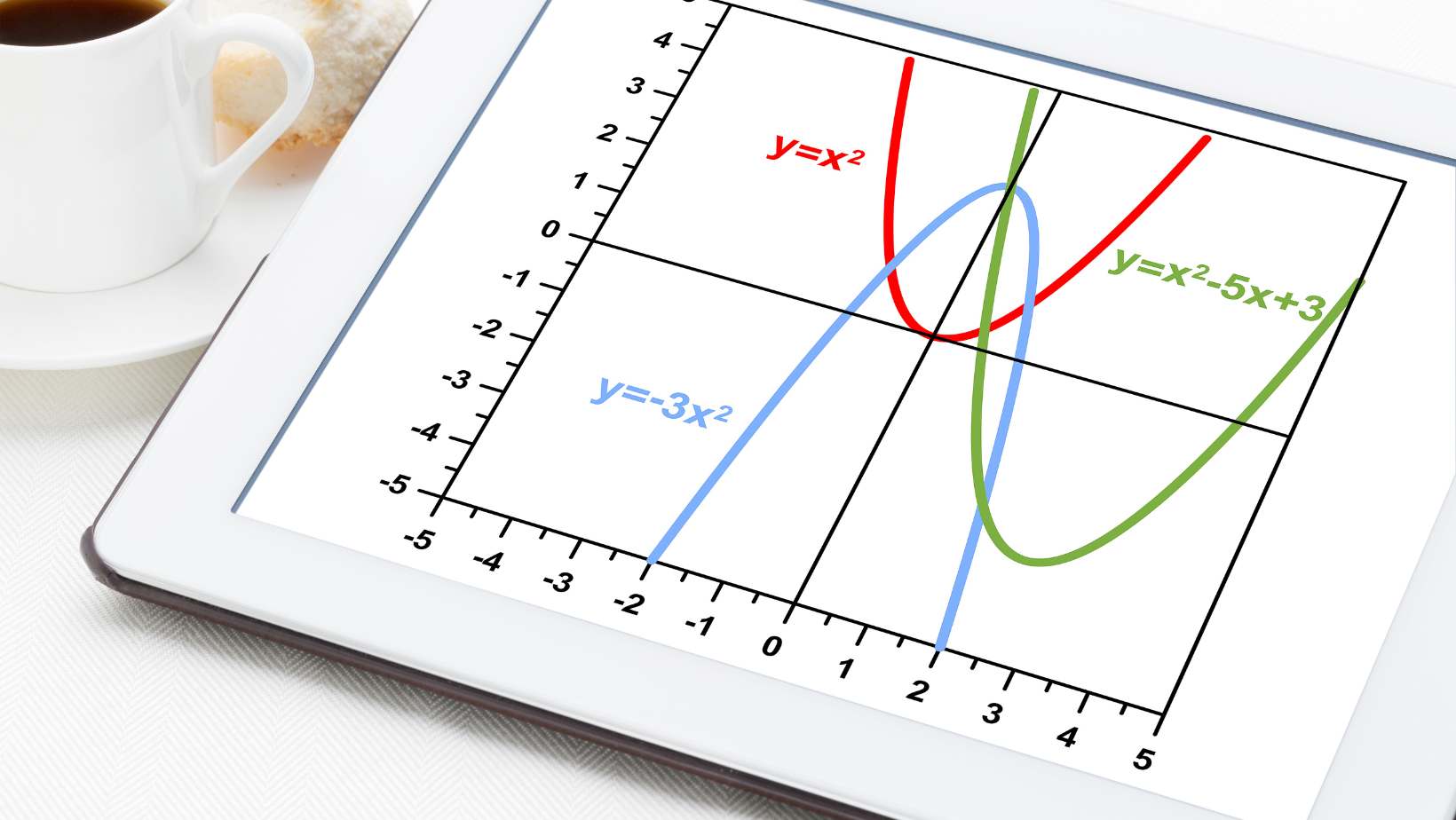
Methods to Identify a Local Minimum
Graph Analysis
When it comes to identifying a local minimum on a graphed function, one effective method is through graph analysis. By visually examining the graph, we can gain valuable insights into the behavior of the function and pinpoint the location of the local minimum. Here are a few steps to follow when analyzing the graph:
- Locate the critical points: Critical points are the points on the graph where the derivative of the function is either zero or undefined. These points can potentially be local minima. Find the x-values of the critical points by setting the derivative of the function equal to zero and solving for x.
- Check the slope: Once you have identified the critical points, determine the slope of the function on either side of each critical point. If the slope changes from negative to positive, it indicates a possible local minimum. This change in slope suggests that the function is transitioning from decreasing to increasing, which is a characteristic of a local minimum.
- Examine the concavity: Another important aspect to consider is the concavity of the function. Determine the concavity by analyzing the second derivative of the function. If the concavity changes from concave down to concave up at a critical point, it indicates the presence of a local minimum. This change in concavity suggests that the function is transitioning from being “curved downward” to being “curved upward,” which is a characteristic of a local minimum.
By carefully analyzing the graph, paying attention to the critical points, slope, and concavity, we can successfully identify a local minimum and gain a deeper understanding of the behavior of the function.
In conclusion, understanding the concept of a local minimum is crucial in mathematics and optimization problems, as it allows for informed decisions and predictions about the behavior of a function. By following specific steps, such as graph analysis and calculus techniques, one can correctly identify a local minimum on a graphed function.